Setiap benda yang bergerak di permukaan bumi pada umumnya adalah gabungan dari energi kinetik dan energi potensial. Gabungan kedua energi tersebut menghasilkan total energi yang disebut sebagai energi mekanik.
Mobil
yang sedang bergerak di jalan raya memiliki energi mekanik. Jika mobil berjalan
di jalan yang datar maka energi potensialnya nol. Namun jika mobil berjalan di
jalan menanjak atau lintasan pada ketinggian tertentu maka mobil tersebut
memiliki energi potensial.
Energi mekanik (Em) = Energi Potensial (Ep)
+ Energi Kinetik (Ek).
Energi potensial
adalah energi yang dimiliki oleh suatu materi karena lokasi atau tempatnya.
Sedangkan Energi kinetik adalah bentuk energi ketika suatu materi berpindah
atau bergerak. Secara matematis energi mekanik dapat
dituliskan pada persamaan berikut:
Em = Ep + Ek
Dengan,
Em = Energi mekanik (Joule)
Ep = Energi
Potensial (Joule)
Ep = m x g x h
Ek = Enegi
kinetik (Joule)
Ek = ½ mv2
Hukum
Kekekalan Energi Mekanik
 |
| Kelapa jatuh dari pohon |
Gambar di atas, menggambarkan buah kelapa yang bermassa 1 kg lepas dari dahannya dan melakukan jatuh bebas dari ketinggian 20 meter di tanah. Jika gerak buah kelapa kita analisa di dapat data seperti pada tabel di bawah ini.
Dari data di atas, selama
buah kelapa jatuh bebas di dapat:
a. Energi potensialnya
mengecil
b. Energi kinetiknya
membesar
c. Energi mekaniknya tetap
Dalam medan gravitasi
konstan, energi mekanik yang dimiliki oleh suatu benda bernilai konstan.
Em1
= Em2
Ek1
+ Ep1 = Ek2 + Ep2
Persamaan tersebut dinamakan
hukum kekekalan energi mekanik.
Hubungan
Energi Potensial dan Energi Kinetik
Pada
sebuah benda yang jatuh bebas, terdapat dua buah energi yaitu energi mekanik.
Energi mekanik terdiri atas energi potensial dan energi kinetik. Meskipun
energi potensial benda yang jatuh bebas akan semakin kecil ketika ketinggian
semakin rendah, tetapi di sisi lain energi kinetiknya bertambah. Dengan
demikian energi mekaniknya tetap sama (konstan). Kekekalan energi mekanik pada
benda jatuh bebas dapat diilustrasikan seperti pada Gambar di bawah ini.
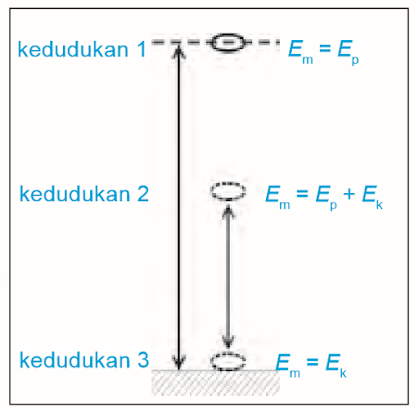 |
| Skema perubahan energi pada benda jatuh |
Pada kedudukan 1, energi mekanik seluruhnya merupakan energi potensial. Dapat dituliskan sebagai berikut.
Em = Ep
= m × g × h
Pada kedudukan 2,
energi mekanik merupakan jumlah energi potensial dan energi kinetik. Dapat
dituliskan sebagai berikut.
Em = Ep
+ Ek = (m × g × h) + (½ × m × v2)
Pada kedudukan 3,
energi mekanik seluruhnya merupakan energi kinetik. Dapat dituliskan sebagai
berikut.
Em = Ek
= ½ × m × v2
Latihan
Soal:
1. Sebuah
benda memiliki energi potensial 100 J jatuh dari ketinggian tertentu. Berapakah
energi kinetik benda saat mencapai tanah?
Jawab: Energi kinetik
adalah energi ketika suatu materi bergerak. Pada saat mencapai tanah, maka
energi kinetik benda tersebut sama dengan 100 J
2. Buah
jambu yang bergantung di ketinggian 2 meter dari tanah, tiba-tiba jatuh. Amir
yang menemukan buah jambu tersebut menimbangnya, ternyata massanya 200 g. Jika
percepatan gravitasi di tempat itu 10 m/s2. Hitunglah:
a.
energi potensial dan energi kinetik yang dimiliki buah jambu ketika masih
bergantung,
b.
energi potensial, energi kinetik dan kecepatan buah jambu pada ketinggian 1
meter,
c.
energi kinetik dan kecepatan saat mencapai tanah
Penyelesaian:
a. Buah jambu ketika masih tergantung 2 meter
Energi
potensial buah jambu ketika masih bergantung 2 meter
Em = Ep
= m × g × h
Em = Ep
= 200 g x 10 m/s2 x 2 m
Em = Ep
= 0,2 kg x 10 m/s2 x 2 m
Em = Ep
= 4 J
Energi
kinetik buah jambu ketika masih bergantung 2 meter
Energi kinetik (Ek)
= 0
b. Ketika buah jambu jatuh pada ketinggian 1 meter
Em = Ep
+ Ek = (m × g × h) + (½ × m × v2)
Energi
potensial pada ketinggian 1 meter
Ep = m x g
x h
Ep = 200 g
x 10 m/s2 x 1 m
Ep = 0,2 kg
x 10 m/s2 x 1 m
Ep = 2 J
Menghitung
kecepatan buah jambu pada ketinggian 1 meter
Em1 =
Em2
Ek1 +
Ep1 = Ek2
+ Ep2
Ek1 = Ep2
+ Ek2
m × g × h1
= m × g × h2 + ½ × m × v2
½ × m × v2 = m × g × h1 - m × g × h2
v2 = 2 × g
× (h1 – h2)
v2 = 2 × 10
m/s2 x (2 m – 1 m)
v2 = 2 × 10
m/s2 x 1 m
v2 = 20
v = 4,47 m/s
Energi
kinetik buah jambu pada ketinggian 1 meter
Ek = ½ × m
× v2
Ek = ½ ×
0,2 kg × 20
Ek = 2 J
c. Energi kinetik dan kecepatan saat mencapai tanah
Kecepatan
saat mencapai tanah
v2 = 2 × g
× (h1 – h2)
v2 = 2 × 10
m/s2 x (2 m – 0 m)
v2 = 40
v = 6,32 m/s
Energi
kinetik saat mencapai tanah
Em = Ek = ½ × m × v2
Ek = ½ × m × v2
Ek = ½ × 0,2 × 40
Ek = 4 Joule
Referensi
Ilmu Pengetahuan Alam SMP Kelas VIII. Kementerian Pendidikan,
Kebudayaan, Riset, dan Teknologi Republik Indonesia, 2021. Penulis: Okky Fajar
Tri Maryana, Dkk. ISBN: 978-602-244-383-4
Ilmu Pengetahuan Alam 2: SMP/MTs Kelas VIII/oleh Wasis, Sugeng
Yuli Irianto. — Jakarta: Pusat Perbukuan, Departemen Pendidikan Nasional, 2008.
Belajar IPA: membuka cakrawala alam sekitar 2 untuk kelas VIII/
SMP/MTs Saeful Karim – Jakarta: Pusat Perbukuan, Departemen Pendidikan
Nasional, 2008.
Fisika : untuk SMA dan MA Kelas XI / penyusun, Tri Widodo. Editor: Widha Sunarno, Arief Satiyo Nugroho ; Pandu, Budi S. Jakarta Pusat Perbukuan, Departemen Pendidikan Nasional, 2009.
Baca juga:
Bab 3 Usaha, Energi, Pesawat Sederhana | |
01 | |
02 | |
03 | |
04 | |
05 | |
06 | |
07 | |
08 | |
09 | |
10 | |
11 | |
12 | |
13 | |
14 | |
15 | |
16 | |
17 | |
18 | |
19 | |
20 | |

Tidak ada komentar:
Posting Komentar